|
|
| Publications |

|
2021
Topological transitions in two-dimensional Floquet superconductors
Paul Wenk, Milena Grifoni, John Schliemann
[arXiv]
Abstract
<--->
We demonstrate the occurrence of a topological phase transition induced by an effective magnetic field in a two-dimensional electron gas with spin-orbit coupling and in proximity to an s-wave superconductor. The effective, perpendicular magnetic field is generated by an in plane, off-resonant ac-magnetic field or by circularly polarized light. The conditions for entering the topological phase do not rely on fine parameter tuning: For fixed frequency, one requires a minimal amplitude of the effective field which can be evaluated analytically. In this phase, chiral edge states generally emerge for a system in stripe geometry unless the Rashba and Dresselhaus coupling have the same magnitude. In this special case, for magnetic field driving the edge states become Majorana flat bands, due to the presence of a chiral symmetry; the light irradiated system is a trivial superconductor.
Many-Body Localization: Transitions in Spin Models
John Schliemann, Joao Vitor I. Costa, Paul Wenk, J. Carlos Egues
Phys. Rev. B 103
174203 (2021), [arXiv]
Abstract
<--->
We
study the transitions between ergodic and many-body localized phases
in spin systems, subject to quenched disorder, including the
Heisenberg chain and the central spin model. In both cases systems
with common spin lengths $1/2$ and 1 are investigated via exact
numerical diagonalization and random matrix techniques. Particular
attention is paid to the sample-to-sample variance $(\Delta_s r)^2$ of
the averaged consecutive-gap ratio $\langle r \rangle$ for different
disorder realizations. For both types of systems and spin lengths we
find a maximum in $\Delta_s r$ as a function of disorder strength,
accompanied by an inflection point of $\langle r \rangle$, signaling
the transition from ergodicity to many-body localization. The critical
disorder strength is found to be somewhat smaller than the values
reported in the recent literature. Further information about the
transitions can be gained from the probability distribution of
expectation values within a given disorder realization.
2020
Persistent spin textures and currents in wurtzite nanowire-based quantum structures
Michael Kammermeier, Adrian Seith,
Paul Wenk, and John Schliemann
Phys. Rev. B 101
195418 (2020), [arXiv]
Abstract
<--->
We explore the spin and charge properties of electrons in wurtzite semiconductor nanowires where radial and axial confinement leads to tubular or ring-shaped quantum structures. Accounting for spin-orbit interaction induced by the wurtzite lattice as well as a radial potential gradient, we analytically derive the corresponding low-dimensional Hamiltonians. It is demonstrated that the resulting tubular spin-orbit Hamiltonian allows to construct spin states that are persistent in time and robust against disorder. We find that these special scenarios are characterized by distinctive features in the optical conductivity spectrum, which enable an unambiguous experimental verification. In both types of quantum structures, we discuss the dependence of the occurring persistent charge and spin currents on an axial magnetic field and Fermi energy which show clear fingerprints of the electronic subband structure. Here, the spin-preserving symmetries become manifest in the vanishing of certain spin current tensor components. Our analytic description relates the distinctive features of the optical conductivity and persistent currents to bandstructure characteristics which allows to deduce spin-orbit coefficients and other band parameters from measurements.
Floquet-Drude
conductivity
Martin Wackerl, Paul Wenk, and John
Schliemann
Phys. Rev. B 101
184204 (2020), [arXiv]
Abstract
<--->
A generalization of the Drude
conductivity for systems which
are exposed to periodic
driving is presented. The
probe bias is treated
perturbatively by using the
Kubo formula, whereas the
external driving is included
nonperturbatively using the
Floquet theory. Using a
different type of four-times
Green functions disorder is
approached diagrammatically,
yielding a fully analytical
expression for the
Floquet-Drude
conductivity. Furthermore, the
Floquet Fermi "golden rule" is
generalized to $t$-$t'$
Floquet states, connecting the
Floquet-Dyson series with
scattering theory for Floquet
states. It is shown that a
low-energy approximation like
the parabolic one fails
significantly to give the
correct conductivity in a
system under driving.
2019
In-plane magnetoelectric response in bilayer graphene
Michael Kammermeier, Paul Wenk, and Ulrich Zülicke
Phys. Rev. B
100, 075421 (2019), [arXiv],
Abstract
<--->
A graphene bilayer shows an unusual magnetoelectric response whose
magnitude is controlled by the valley-isospin density, making it
possible to link magnetoelectric behavior to
valleytronics. Complementary to previous studies, we consider the
effect of static homogeneous electric and magnetic fields that are
oriented parallel to the bilayer's plane. Starting from a
tight-binding description and using quasi-degenerate perturbation
theory, the low-energy Hamiltonian is derived including all relevant
magnetoelectric terms whose prefactors are expressed in terms of
tight-binding parameters. We confirm the existence of an expected
axion-type pseudoscalar term, which turns out to have the same sign
and about twice the magnitude of the previously obtained out-of-plane
counterpart. Additionally, small anisotropic corrections to the
magnetoelectric tensor are found that are fundamentally related to the
skew interlayer hopping parameter $\gamma_4$. We discuss possible ways to
identify magnetoelectric effects by distinctive features in the
optical conductivity.
Driven Hofstadter butterflies and related topological invariants
Martin Wackerl, Paul Wenk, and John Schliemann
Phys. Rev. B
100, 165411 (2019), [arXiv],
Abstract
<--->
The properties of the Hofstadter butterfly, a fractal, self-similar
spectrum of a two-dimensional electron gas, are studied in the case
where the system is additionally illuminated with monochromatic
light. This is accomplished by applying Floquet theory to a
tight-binding model on the honeycomb lattice subjected to a
perpendicular magnetic field and either linearly or circularly
polarized light. It is shown how the deformation of the fractal
structure of the spectrum depends on intensity and
polarization. Thereby, the topological properties of the Hofstadter
butterfly in the presence of the oscillating electric field are
investigated. A thorough numerical analysis of not only the Chern
numbers but also the $W3$ invariants gives the appropriate insight into
the topology of this driven system. This includes a comparison of a
direct $W_3$ calculation to the method based on summing up Chern numbers
of the truncated Floquet Hamiltonian.
Ultralong spin lifetimes in one-dimensional semiconductor nanowires
Florian Dirnberger, Michael Kammermeier, Jan
König, Moritz Forsch, Paulo E. Faria Junior, Tiago Campos,
Jaroslav Fabian, John Schliemann, Christian Schüller, Tobias
Korn, Paul Wenk, and Dominique Bougeard
Appl. Phys. Lett. 114,
202101 (2019), [arXiv],
Abstract
<--->
We experimentally demonstrate ultralong spin lifetimes of electrons in
the one-dimensional (1D) quantum limit of semiconductor
nanowires. Optically probing single wires of different diameters
reveals an increase in the spin relaxation time by orders of magnitude
as the electrons become increasingly confined until only a single 1D
subband is populated. We find the observed spin lifetimes of more than
200ns to result from the robustness of 1D electrons against major spin
relaxation mechanisms, highlighting the promising potential of these
wires for long-range transport of coherent spin information.
2018
Spin relaxation in wurtzite nanowires
Michael Kammermeier, Paul Wenk, Florian Dirnberger, Dominique Bougeard, and John
Schliemann
Phys. Rev. B
98, 035407 (2018),
[arXiv]
.
Abstract
<--->
We theoretically investigate the D'yakonov-Perel' spin relaxation
properties in diffusive wurtzite semiconductor nanowires and their
impact on the quantum correction to the conductivity. Although the
lifetime of the long-lived spin states is limited by the dominant
$k$-linear spin-orbit contributions in the bulk, these terms show almost
no effect in the finite-size nanowires. Here, the spin lifetime is
essentially determined by the small $k$-cubic spin-orbit terms and
nearly independent of the wire radius. At the same time, these states
possess in general a complex helical structure in real space that is
modulated by the spin precession length induced by the $k$-linear
terms. For this reason, the experimentally detected spin relaxation
largely depends on the ratio between the nanowire radius and the spin
precession length as well as the type of measurement. In particular,
it is shown that while a variation of the radius hardly affects the
magnetoconductance correction, which is governed by the long-lived
spin states, the change in the spin lifetime observed in optical
experiments can be dramatic.
Add-on: Talk
by F. Dirnberger about spin dynamics in single GaAs
nanowires
2017
Magnetoconductance correction in zinc-blende semiconductor nanowires with spin-orbit coupling
Michael Kammermeier, Paul Wenk, John
Schliemann, Sebastian Heedt, Thomas Gerster, and Thomas Schäpers
Phys. Rev. B 96,
235302 (2017),
[arXiv]
Abstract
<--->
We study the effects of spin-orbit coupling on the magnetoconductivity
in diffusive cylindrical semiconductor nanowires. Following up on our
former study on tubular semiconductor nanowires, we focus in this
paper on nanowire systems where no surface accumulation layer is
formed but instead the electron wave function extends over the entire
cross section. We take into account the Dresselhaus spin-orbit
coupling resulting from a zinc-blende lattice and the Rashba
spin-orbit coupling, which is controlled by a lateral gate
electrode. The spin relaxation rate due to Dresselhaus spin-orbit
coupling is found to depend neither on the spin density component nor
on the wire growth direction and is unaffected by the radial
boundary. In contrast, the Rashba spin relaxation rate is strongly
reduced for a wire radius that is smaller than the spin precession
length. The derived formulas are fitted to the data of
magnetoconductance measurements of a heavily-doped back-gated InAs
nanowire and transport parameters are extracted.
Add-on: Talk
2016
Control of spin helix symmetry in semiconductor
quantum wells by crystal orientation
Michael Kammermeier, Paul Wenk, and John
Schliemann
Phys. Rev. Lett. 117,
236801 (2016) (on the cover),
[arXiv]
, [POSTER],
Media release of the University of Regensburg (in German).
Abstract
<--->
We investigate the possibility of spin-preserving symmetries due to
the interplay of Rashba and Dresselhaus spin-orbit coupling in n-doped
zinc-blende semiconductor quantum wells of general crystal
orientation. It is shown that a conserved spin operator can be
realized if and only if at least two growth-direction Miller indices
agree in modulus. The according spin-orbit field has in general both
in-plane and out-of-plane components and is always perpendicular to
the shift vector of the corresponding persistent spin helix. We also
analyze higher-order effects arising from the Dresselhaus term, and
the impact of our results on weak (anti)localization corrections.
Weak (Anti-)Localization in Tubular
Semiconductor Nanowires with Spin-Orbit Coupling
Michael Kammermeier, Paul Wenk, John Schliemann,
Sebastian Heedt, and Thomas Schäpers
Phys. Rev. B 93,
205306 (2016) (Editor´s Suggestion),
[arXiv]
Abstract
<--->
We compute analytically the weak (anti-)localization correction to the
Drude conductivity for electrons in tubular semiconductor systems of
zinc blende type. We include linear Rashba and Dresselhaus spin-orbit
coupling (SOC) and compare wires of standard growth directions <100>,
<111> and <110>. The motion on the quasi-two-dimensional surface is
considered diffusive in both directions: transversal as well as along
the cylinder axis. It is shown that Dresselhaus and Rashba SOC
similarly affect the spin relaxation rates. For the <110> growth
direction the long-lived spin states are of helical nature. We detect
a crossover from weak localization to weak anti-localization depending
on spin-orbit coupling strength as well as dephasing and scattering
rate. The theory is fitted to experimental data of an undoped <111>
InAs nanowire device which exhibits a top-gate-controlled crossover
from positive to negative magnetoconductivity. Thereby, we extract
transport parameters where we quantify the distinct types of SOC
individually.
Add-on: Talk
Trigonal Warping in Bilayer Graphene: Energy
versus Entanglement Spectrum
Sonja Predin, Paul Wenk, and John
Schliemann
Phys. Rev. B 93,
115106 (2016), [arXiv]
Abstract
<--->
We present a mainly analytical study of the entanglement spectrum of
Bernal-stacked graphene bilayers in the presence of trigonal warping
in the energy spectrum. Upon tracing out one layer, the entanglement
spectrum shows qualitative geometric differences to the energy
spectrum of a graphene monolayer. However, topological quantities such
as Berry-phase-type contributions to Chern numbers agree. The latter
analysis involves not only the eigenvalues of the entanglement
Hamiltonian but also its eigenvectors. We also discuss the
entanglement spectra resulting from tracing out other sublattices. As
a technical basis of our analysis, we provide closed analytical
expressions for the full eigensystem of bilayer graphene in the entire
Brillouin zone with a trigonally warped spectrum.
Conserved Spin Quantity in Strained Hole
Systems with Rashba and Dresselhaus Spin-Orbit
Coupling
Paul Wenk, Michael Kammermeier, and John
Schliemann
Phys. Rev. B 93,
115312 (2016), [arXiv]
, [POSTER]
Abstract
<--->
We derive an effective Hamiltonian for a (001)-confined
quasi-two-dimensional hole gas in a strained zinc-blende semiconductor
heterostructure including both Rashba and Dresselhaus spin-orbit
coupling. In the presence of uniaxial strain along the <110> axes, we
find a conserved spin quantity in the vicinity of the Fermi contours
in the lowest valence subband. In contrast to previous works, this
quantity meets realistic requirements for the Luttinger
parameters. For more restrictive conditions, we even find a conserved
spin quantity for vanishing strain, restricted to the vicinity of the
Fermi surface.
Add-on: Talk
Ballistic and spin transport in InAs nanowires
Th. Schapers, S. Heedt, A. Bringer, H. Hardtdegen, J. Schubert, D. Grutzmacher, M. Kammermeier, P. Wenk, J. Schliemann, W. Prost
IEEE Nanotechnology Materials and Devices Conference (2016)
Abstract
<--->
The transport in InAs nanowires is investigated at low
temperatures. On wires with different n-type doping information on
Rashba and Dresselhaus spin-orbit coupling is gained from weak
antilocalization measurements. By using a short local gate quantum
point contacts are formed, which show quantized conductance. From
bias-depended measurements the g-factor is extracted for different
subbands.
2015
Lifetimes of Magnons in Two-Dimensional Diluted
Ferromagnetic Systems
Akash Chakraborty, Paul Wenk, and John
Schliemann
Eur. Phys. J. B 88,
64 (2015),
[arXiv]
Abstract
<--->
Spin dynamics in low dimensional magnetic systems has been of
fundamental importance for a long time and has currently received an
impetus owing to the emerging field of nanoelectronics. Knowledge of
the spin wave lifetimes, in particular, can be favorable for future
potential applications. We investigate the low-temperature spin wave
excitations in two-dimensional disordered ferromagnetic systems, with
a particular focus on the long wavelength magnon lifetimes. A
semi-analytical Green's functions based approach is used to determine
the dynamical spectral functions, for different magnetic impurity
concentrations, from which the intrinsic linewidth is extracted. We
obtain an unambiguous
$q^4$
scaling of the magnon linewidth which is ascribed to the disorder
induced damping of the spin waves, thereby settling a longstanding
unresolved issue on the wave-vector dependence. Our findings are also
in good agreement with previous theoretical studies on Heisenberg
ferromagnets. Additionally, we demonstrate the futility of using the
low moments associated with the spectral densities to evaluate the
magnon dispersions and lifetimes.
2014
Signatures of spin-preserving symmetries in
two-dimensional hole gases
Tobias Dollinger, Michael Kammermeier, Andreas
Scholz, Paul Wenk, John Schliemann, Klaus Richter, and Roland
Winkler
Phys. Rev. B 90,
115306 (2014).
Abstract
<--->
We investigate ramifications of the persistent spin helix symmetry in
two-dimensional hole gases in the conductance of disordered mesoscopic
systems. To this end we extend previous models by going beyond the
axial approximation for III-V semiconductors. For heavy-hole subbands
we identify an exact spin-preserving symmetry analogous to the
electronic case by analyzing the crossover from weak antilocalization
to weak localization and spin transmission as a function of extrinsic
spin-orbit interaction strength.
Spin-wave excitations in presence of
nanoclusters of magnetic impurities
Akash Chakraborty, Paul Wenk, Stefan Kettemann,
Richard Bouzerar, Georges Bouzerar
New
J. Phys. 16, 033004 (2014), [arXiv]
Abstract
<--->
Nanoscale inhomogeneities and impurity clustering are often found to
drastically affect the magnetic and transport properties in
disordered/diluted systems, giving rise to rich and complex
phenomena. However, the physics of these systems still remains to be
explored in more detail as can be seen from the scarce literature
available. We present a detailed theoretical analysis of the effects
of nanoscale inhomogeneities on the spin excitation spectrum in
diluted magnetic systems. The calculations are performed on relatively
large systems (up to
$N=66^3$). It is found that even low concentrations of
inhomogeneities have drastic effects on both the magnon density of
states and magnon excitations. These effects become even more
pronounced in the case of short-ranged magnetic interactions between
the impurities. In contrast to the increase of critical temperatures
$T_C$,
reported in previous studies, the spin-stiffness $D$ is systematically
suppressed in the presence of nanoscale inhomogeneities. Moreover D is
found to strongly depend on the inhomogeneities' concentration, the
cluster size, as well as the range of the magnetic interactions. The
findings are discussed in the prospect of potential spintronics
applications. We believe that this detailed numerical work could
initiate future experimental studies to probe this rich physics with
the most appropriate tool, inelastic neutron scattering.
Spin injection and spin-orbit coupling in
low-dimensional semiconductor nanostructures
Sebastian Heedt, Isabel Wehrmann, Thomas Gerster, Paul Wenk, Stefan Kettemann, Kamil Sladek, Hilde Hardtdegen, Andreas Bringer, Jürgen Schubert, Natalia Demarina, Detlev Grützmacher, Thomas Schäpers
in
Spintronics VII, SPIE (2014)
Abstract
<--->
Due to their strong spin-orbit coupling III-V semiconductor nanowires
are excellent candidates for electrical spin manipulation. Therefore,
a major goal is to tailor spin-orbit coupling in these devices. Direct
electrical spin injection into quasi one-dimensional nanowires is
demonstrated. Furthermore, the weak antilocalization effect was
investigated in InAs nanowires. The quantum corrections to the
conductivity are interpreted by developing a quasi-one-dimensional
diffusive model. It turns out that by means of doping and electric
gating the spin-lifetimes can be tuned significantly. By creating
few-electron quantum dots inside these devices the impact of the
confinement on the spin relaxation properties is investigated.
2013
Plasmons in spin-orbit coupled two-dimensional
hole gas systems
Andreas Scholz, Tobias Dollinger, Paul Wenk,
Klaus Richter, and John Schliemann
Phys. Rev. B 87,
085321 (2013).
Abstract
<--->
We study the dynamical dielectric function of a two-dimensional hole
gas, exemplified on [001] GaAs and InAs quantum wells, within the
Luttinger model extended to the two lowest subbands including bulk and
structure inversion asymmetric terms. The plasmon dispersion shows a
pronounced anisotropy for GaAs- and InAs-based systems. In GaAs this
leads to a suppression of plasmons due to Landau damping in some
orientations. Due to the large Rashba contribution in InAs, the
lifetime of plasmons can be controlled by changing the electric
field. This effect is potentially useful in plasmon field effect
transistors as previously proposed for electron gases.
2012
Spontaneous magnetization in the presence of nanoscale inhomogeneities in diluted magnetic systems
Akash Chakraborty, Paul Wenk, Richard Bouzerar, and Georges Bouzerar
Phys. Rev. B 86,
214402 (2012), [arXiv]
Add-on: Talk
by A. Chakraborty
Abstract
<--->
The presence of nanoscale inhomogeneities has been experimentally
evidenced in several diluted magnetic systems, which in turn often
leads to interesting physical phenomena. However, a proper theoretical
understanding of the underlying physics is lacking in most of the
cases. Here, we present a detailed and comprehensive theoretical study
of the effects of nanoscale inhomogeneities on the
temperature-dependent spontaneous magnetization in diluted magnetic
systems, which is found to exhibit an unusual and unconventional
behavior. The effects of impurity clustering on the magnetization
response have hardly been studied until now. We show that nanosized
clusters of magnetic impurities can lead to drastic effects on the
magnetization compared to that of homogeneously diluted compounds. The
anomalous nature of the magnetization curves strongly depends on the
relative concentration of the inhomogeneities as well as the effective
range of the exchange interactions. In addition, we also provide a
systematic discussion of the nature of the distributions of the local
magnetizations.
Spin Hall conductivity on the anisotropic triangular lattice
Paul Wenk, Stefan Kettemann, and Georges Bouzerar
Phys. Rev. B 86,
075441 (2012), [arXiv]
Abstract
<--->
We present a detailed study of the spin Hall conductivity on a
ballistic two-dimensional triangular lattice in the presence of Rashba
spin-orbit coupling. In particular, we focus part of our attention on
the effect of the anisotropy of the nearest neighbor hopping
amplitude. It is found that the presence of anisotropy has drastic
effects on the spin Hall conductivity, especially in the hole doped
regime where a significant increase or/and reversed sign of the spin
Hall conductivity has been obtained. We also provide a systematic
analysis of the numerical results in terms of Berry phases. The
changes of signs observed at particular density of carriers appear to
be a consequence of both Fermi surface topology and change of sign of
electron velocity. In addition, in contrast to the two-dimensional
square lattice, it is shown that the tight binding spin-orbit
Hamiltonian should be derived carefully from the continuous model on
the triangular lattice.
2011
Direction dependence of spin relaxation in
confined two-dimensional systems
Paul Wenk, and Stefan Kettemann
Phys. Rev. B 83,
115301
(2011), [World Scientiffic (Open Access)]
, [POSTER]
Abstract
<--->
The dependence of spin relaxation on the direction of the quantum wire
under Rashba and Dresselhaus (linear and cubic) spin-orbit coupling is
studied. Comprising the dimensional reduction of the wire in the
diffusive regime, the lowest spin relaxation and dephasing rates for
(001) and (110) systems are found. The analysis of spin relaxation
reduction is then extended to nondiffusive wires where it is shown
that, in contrast to the theory of dimensional crossover from weak
localization to weak antilocalization in diffusive wires, the
relaxation due to cubic Dresselhaus spin-orbit coupling is reduced and
the linear part is shifted with the number of transverse channels.
2010
Dimensional dependence of weak localization
corrections and spin relaxation in quantum wires with Rashba
spin-orbit coupling
Paul Wenk, and Stefan Kettemann
Phys. Rev. B 81,
125309
(2010), [arXiv]
, [POSTER]
Abstract
<--->
The quantum correction to the conductivity in disordered quantum wires
with linear Rashba spin-orbit coupling is obtained. For quantum wires
with spin-conserving boundary conditions, we find a crossover from
weak antilocalization to weak localization as the wire width W is
reduced using exact diagonalization of the Cooperon equation. This
crossover is due to the dimensional dependence of the spin relaxation
rate of conduction electrons, which becomes diminished, when the wire
width W is smaller than the bulk spin precession length LSO. We thus
confirm previous results for small wire width,
$W/L_\text{SO}\lesssim 1$ [S. Kettemann,
Phys. Rev. L 98, 176808 (2007)], where only the transverse 0
modes of the Cooperon equation had been taken into account. We find
that spin helix solutions become stable for arbitrary ratios of linear
Rashba and Dresselhaus coupling in narrow wires. For wider wires, the
spin relaxation rate is found to be not monotonous as function of wire
width $W$: it becomes first enhanced for $W$ on the order of the bulk spin
precession length
$W/L_\text{SO}$ before it becomes diminished for smaller wire widths. In
addition, we find that the spin relaxation is smallest at the edge of
the wire for wide wires. The effect of the Zeeman coupling to the
magnetic field perpendicular to the 2D electron system (2DES) is
studied and found to result in a modification of the
magnetoconductivity: it shifts the crossover from weak
antilocalization to weak localization to larger wire widths
$W_c$. When
the transverse confinement potential of the quantum wire is smooth,
the boundary conditions become rather adiabatic. Then, the spin
relaxation rate is found to be enhanced as the wire width W is
reduced. We find that only a spin-polarized state retains a finite
spin relaxation rate in such narrow wires. Thus, we conclude that the
injection of polarized spins into nonmagnetic quantum wires should be
favorable in wires with smooth confinement potential. Finally, in
wires with tubular shape, corresponding to transverse periodic
boundary conditions, we find no reduction of the spin relaxation rate.
Spin Relaxation in Quantum Wires
Paul Wenk, and Stefan Kettemann
In: Handbook of Nanophysics: Nanotubes and Nanowires by
K. Sattler (2010), [arXiv]
Abstract
<--->
The spin dynamics and spin relaxation of itinerant electrons in
quantum wires with spin-orbit coupling is reviewed. We give an
introduction to spin dynamics, and review spin-orbit coupling
mechanisms in semiconductors. The spin diffusion equation with
spin-orbit coupling is derived, using only intuitive, classical random
walk arguments. We give an overview of all spin relaxation mechanisms,
with particular emphasis on the motional narrowing mechanism in
disordered conductors, the D'yakonov-Perel'-Spin relaxation. Here, we
discuss in particular, the existence of persistent spin helix
solutions of the spin diffusion equation, with vanishing spin
relaxation rates. We then, derive solutions of the spin diffusion
equation in quantum wires, and show that there is an effective
alignment of the spin-orbit field in wires whose width is smaller than
the spin precession length
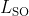 . We show that the resulting reduction in the spin
relaxation rate results in a change in the sign of the quantum
corrections to the conductivity. Finally, we present recent
experimental results which confirm the decrease of the spin relaxation
rate in wires whose width is smaller than . We show that the resulting reduction in the spin
relaxation rate results in a change in the sign of the quantum
corrections to the conductivity. Finally, we present recent
experimental results which confirm the decrease of the spin relaxation
rate in wires whose width is smaller than
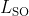 : the direct optical measurement of the spin relaxation
rate, as well as transport measurements, which show a dimensional
crossover from weak antilocalization to weak localization as the wire
width is reduced. Open problems remain, in particular in narrower,
ballistic wires, were optical and transport measurements seem to find
opposite behavior of the spin relaxation rate: enhancement,
suppression, respectively. We conclude with a review of these and
other open problems which still challenge the theoretical
understanding and modeling of the experimental results. : the direct optical measurement of the spin relaxation
rate, as well as transport measurements, which show a dimensional
crossover from weak antilocalization to weak localization as the wire
width is reduced. Open problems remain, in particular in narrower,
ballistic wires, were optical and transport measurements seem to find
opposite behavior of the spin relaxation rate: enhancement,
suppression, respectively. We conclude with a review of these and
other open problems which still challenge the theoretical
understanding and modeling of the experimental results.
Spin Polarized Transport and Spin Relaxation in Quantum Wires
Paul Wenk, Masayuki Yamamoto, Jun-ichiro Ohe, Tomi
Ohtsuki, Bernhard Kramer, Stefan Kettemann
Part of the NanoScience and Technology book series (NANO) (2010), [book link]
Abstract
<--->
We give an introduction to spin dynamics in quantum wires. After a
review of spin-orbit coupling (SOC) mechanisms in semiconductors, the
spin diffusion equation with SOC is introduced. We discuss the
particular conditions in which solutions of the spin diffusion
equation with vanishing spin relaxation rates exist, where the spin
density forms persistent spin helices. We give an overview of spin
relaxation mechanisms, with particular emphasis on the motional
narrowing mechanism in disordered conductors, the D'yakonov-Perel'
spin relaxation. The solution of the spin diffusion equation in
quantum wires shows that the spin relaxation becomes diminished when
reducing the wire width below the spin precession length $L_{\text{SO}}$. This
corresponds to an effective alignment of the spin-orbit field in
quantum wires and the formation of persistent spin helices whose form
as well as amplitude is a measure of the particular SOCs, the linear
Rashba and the linear Dresselhaus coupling. Cubic Dresselhaus coupling
is found to yield in diffusive wires an undiminished contribution to
the spin relaxation rate, however. We discuss recent experimental
results which confirm the reduction of the spin relaxation rate. We
next review theoretical proposals for creating spin-polarized currents
in a T-shape structure with Rashba-SOC. For relatively small SOC, high
spin polarization can be obtained. However, the corresponding
conductance has been found to be small. Due to the self-duality of the
scattering matrix for a system with spin-orbit interaction, no spin
polarization of the current can be obtained for single-channel
transport in two-terminal devices. Therefore, one has to consider at
least a conductor with three terminals. We review results showing that
the amplitude of the spin polarization becomes large if the SOC is
sufficiently strong. We argue that the predicted effect should be
experimentally accessible in InAs. For a possible experimental
realization of InAs spin filters,
see [1].
Thesis
Itinerant Spin Dynamics
in Structures of Reduced Dimensionality
Updated
version (V2, 15.02.18).
Last modified: Do 27. Mai 18:31:13 CEST 2021
|
|

