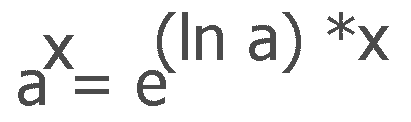https://homepages.uni-regensburg.de/~erc24492/

17.05.2022

MATHE Infos.

wer versteht den Witz?

Empfehlung:
Vorlesungen zu Mathe Themen. SEHR INTERESSANT !!
1. auf deutsch WEITZ --> Mathematiker in Hamburg
       Youtube Kanal: https://www.youtube.com/channel/UCjTfChr0yyz4iZq0x12Q6xA
                                https://www.youtube.com/channel/UCjTfChr0yyz4iZq0x12Q6xA/videos
Bsp. Weihnachtsvorlesung Riemannsche Vermutung
https://www.youtube.com/results?search_query=weitz+weihnachtsvorlesung

2. 3Blue1Brown :auf englisch
https://www.youtube.com/c/3blue1brown
        Youtube Kanal: https://www.youtube.com/c/3blue1brown
    Bsp. https://www.youtube.com/watch?v=d-o3eB9sfls

https://arxiv.org/

3. MathemaTrick: https://www.youtube.com/channel/UCMZgTsrg4GbC7meNeOL86fg
Begreifbare, nachvollziehbare Schritte zur Lösung von Mathe Aufgaben, Algebra, Binome, Integrale. usw.
Macht wirklich Spaß.
Es nimmt die Angst vor Mathematik, denn es wird halt überall mit Wasser gekocht.

Aufgabe:
#Leiter_an_Wand_und_Wuerfel

Sonstiges:
https://www.spektrum.de/news/atiyah-praesentiert-angeblichen-beweis-der-riemannschen-vermutung/1593390

Dreiecke Sinus Cosinus Tangens mit Gaga Hühnerhof AG
Hervorragend erklärt von MathemaTrick https://www.youtube.com/watch?v=YNCo1M7BNHE&t=935s
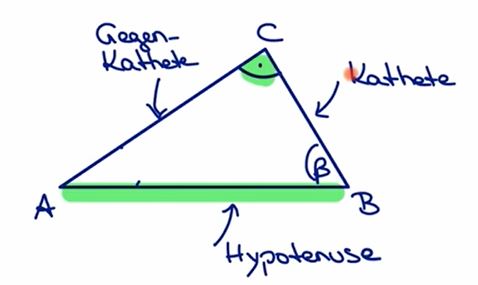
Begriffe:
G=Gegenkathete, A= Ankathete, H=Hypotenuse, W= Winkel Formel
GAGA
HHAG   = Hühnerhof AG   Sprich "Ggaga Hühnerhof AG"
Dabei braucht man den "COTangens eigentlich nicht, Deshalb die Klammer

Winkel Arcus Sin (alpha) =   (Arcus = auch sin^-1 geschrieben (Second fiunktion von sin auf dem Taschenrechner )

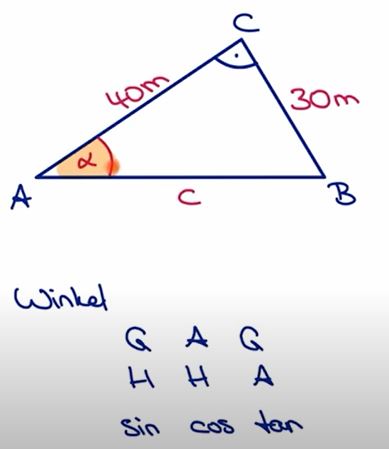
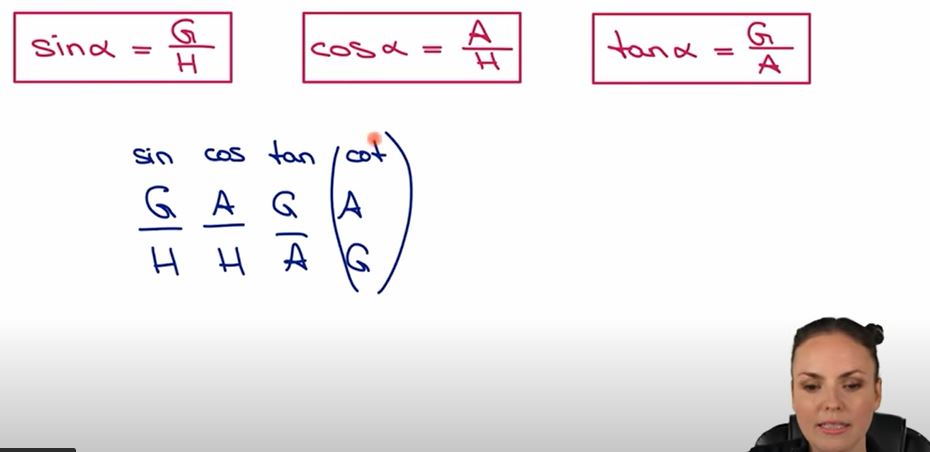
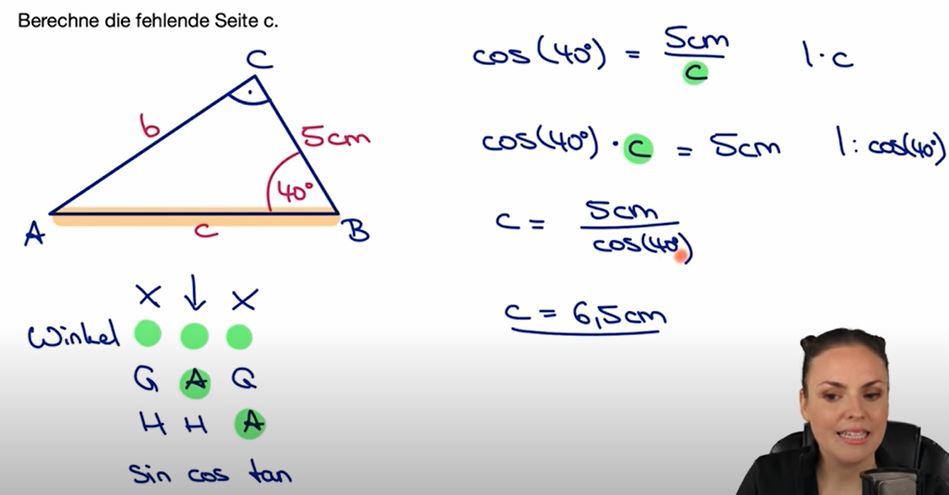
Jetzt Werte eintragen, und da, wo ZWEI grüne Punkte sidn, kann berechnet werden

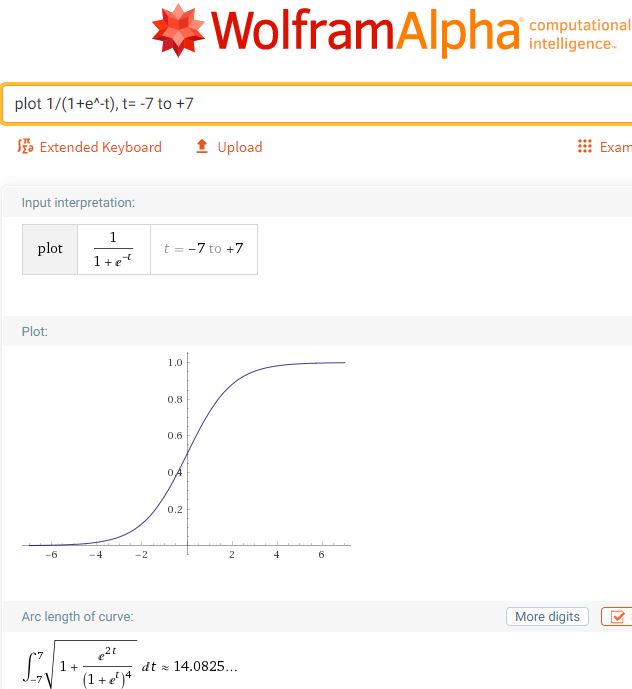
Wolfram Alpha
So schön und einfach kann man Funktionen darstellen .
Hier die im neuronalen Netzen wichtige Sigmoid Funktion
https://www.wolframalpha.com/input/?i=plot+1%2F%281%2Be%5E-t%29%2C+t%3D+-5+to+%2B5

Wichtig: Algebra_Regeln.pdf

Thema:
Notwendigkeit der Logarithmen als schulisches Lernziel: Logarithmen.pdf 06.05.2018
( Komplexe Zahlen würden auch nicht schaden, C.E. )

Fungrube:

#define ROUND(x) ((static_cast<INT) (x+ 0.5)) oder
#define ROUND(x) ((int) (x+ 0.5))
#define M_PI =   in <math.h>   falls der Compiler "C99" Standard hat.
#define M_E   2.7182818284590452354
sonst:
#define MY_PI 3.1415926

const PI_T    (4*atan(1.0))
const double M_PI = 4*atan(1.0);

    printf("PI=%f", M_PI);

A Hoch X :

Nachbildung mit einfachen e-Funktionen:
M_E = 2.7182818,
Natürlicher Logarithmus ln(x)   = e^x
b=ln(a)
a=exp(b)
        für a>0 exp(0)=1

ANSI_C:
zur Basis e

double log ( double __x )

zur Basis 10

double log10 ( double __x )

The function pow() returns the value of __x to the exponent __y

double pow	(	double	__x,
		double	__y
	)

The exp() function returns the exponential value of __x.

double exp ( double __x )

Ersetzt (µController Speicherintensives) pow(x)
a^x= e^((ln a)*x)

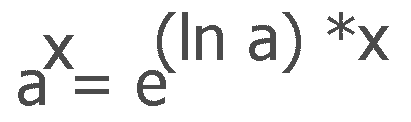
Ausfühung in der Programmiersprace C:   return exp( log(a) * x);   // natürlicher Logarithmus

In ANSI-C bereits definiert:
#include <math.h>
#define     M_E   2.7182818284590452354

// a^x= e^((ln dA)* dX)
// als #define MAKRO
#define A_HOCH_X(DA,DX) (exp(log((double)(DA))* ((double)(DX))))

oder als Funktion:
// *********************************
double AhochX(double dA, double dX)
// *********************************
{
// a^x= e^((ln dA)* dX)
return exp( log(dA) * dX);       // nicht log10(double x)
//Merke: natürlicher Logarithmus in "C" = log(x) nicht log10(x)
};

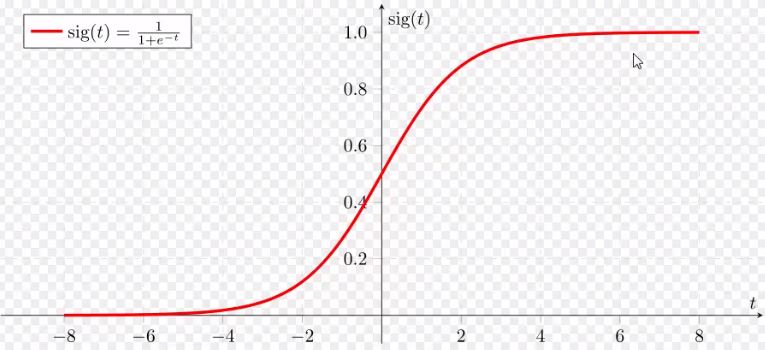
Sigmoid ist "Smoothe" E-Funktion.. X-6..+6 und Y-->= 0..1

Anwendung: Wieche 0..1 Übergänge... dafür gibt es enormen Bedarf.. z.B. Sensorauswertungen etc.
Sigmoid(t) = 1/ 1+(e^-t)
kurz:
// *********************************
float Sigmoid( float fXX)
// *********************************
{
return 1 / (1 + exp( -1*(fXX) ) );
};

QuellFile für DEV_CPP : SigmoidFunction.zip

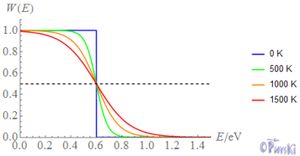
Siehe auch Ähnlichkeit zu der Fermi Verteilung. Diese geht jedoch fallend:
W(E)=1eE−ϵFkBT+1
Darin ist ϵF die Fermi-Energie und W(E) die Besetzungswahrscheinlichkeit.

E= XACh
    1/(e^0 +1
    bzw .
    W(E) = 1 / ( exp( E-µ/kbT ) +1)
    KbT = Termische Energie
    Boltzmankonstante = kb = 8,6173303 (50) * 10^-5 eV/K

Das finde ich sehr spannend:

Was man in C immer braucht:
#include "pch.h"
#include <windows.h>
#include <iostream>
#include <limits>
#include <stdexcept>
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <math.h>
#include <complex> // Wichig ohne .h
#include "main.h"

using namespace std;
//GLOBAL
HWND hWnd;
HDC hDC;
hWnd = GetConsoleWindow();
if( hWnd != NULL ){ MoveWindow(hWnd ,200,10 ,WINX_WIDTH+100, WINY_WIDTH+60 ,TRUE); }
hDC = GetDC(hWnd);

while (getchar() != 'x');
    system("pause");
    ReleaseDC(hWnd, hDC);
    DeleteDC(hDC);

#define COULOUR_MAX_VAL    16777216UL

// Nur ein Beispiel:
SetPixel(hDC, C_Zeta.real() * VERGROESSERUNGSGFAKT + WINX_H, C_Zeta.imag() * VERGROESSERUNGSGFAKT + WINY_H, RGB(220, 220, 220));

#define gotoxy(x,y) printf("\033[%d;%dH", (x), (y)) // Nicht sicher im Anspringen von X/Y

//besser als #define gotoxy(x,y) printf("\033[%d;%dH", (x), (y))
// *********************************
void gotoxy(int x, int y)
// *********************************
{
    char essq[100]; // String variable to hold the escape sequence
    char xstr[100]; // Strings to hold the x and y coordinates
    char ystr[100]; // Escape sequences must be built with characters/
    // ** Convert the screen coordinates to strings
    sprintf_s(xstr, "%d", x);
    sprintf_s(ystr, "%d", y);
    //   ** Build the escape sequence (vertical move)
    essq[0] = '\0';
    strcat_s(essq, "\033[");
    strcat_s(essq, ystr);
    // ** Described in man terminfo as vpa=\E[%p1%dd ** Vertical position absolute
    strcat_s(essq, "d");
    // ** Horizontal move ** Horizontal position absolute
    strcat_s(essq, "\033[");
    strcat_s(essq, xstr);
    // Described in man terminfo as hpa=\E[%p1%dG
    strcat_s(essq, "G"); // ** Execute the escape sequence ** This will move the cursor to x, y
    printf("%s", essq);
}

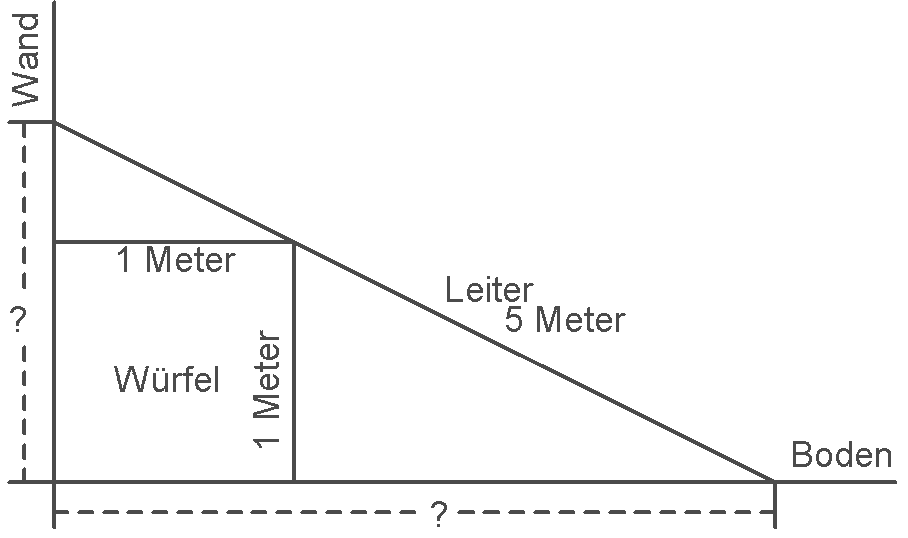
Kleine (grössere) Aufgabe: Leiter, Würfel, Wand und Boden
1 .Ein 1+1 Meter Würfel steht an einer Wand.
2. Eine 5 Meter lange Leiter wird so angelegt, dass Wand, Würfelecke und Boden sich berühren.

Sieht nach einfachen Pythagoras aus. Doch siehe selbst: Tipp: es wird etwas binomisch..

Bedingung:
? Welche Strecke ist von der Wand zur Leiter ?
? Wie hoch liegt die Leiter an der Wand an ?
? Wie kann die Leiter noch angelegt werden ?
( Welche Randbedingung gibt es für die Länge der Leiter ? ) Beweisführung!
.. Bsp Eine 2 Meter Leiter kann ich an den Würfe nur anlehnen.