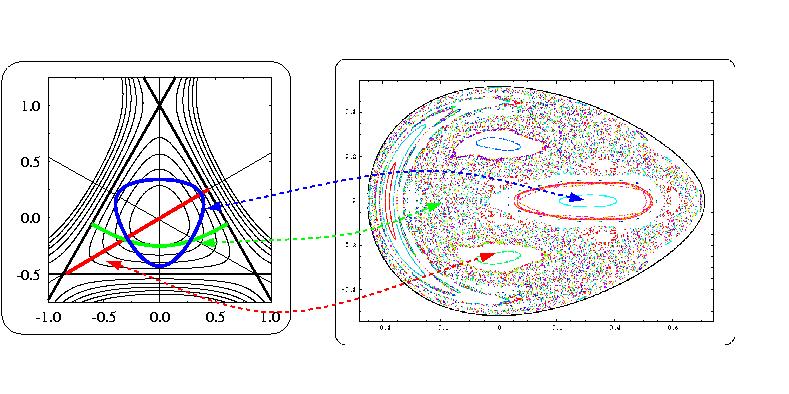
Many quantum phenomena in fermion systems can be described semiclassically. Examples are shell effects in the energies and deformations of atomic nuclei and metal clusters, or oscillations in the transport properties (such as the magneto-resistance) of semiconductor quantum dots and nanostructures. In the semiclassical theory, the periodic orbits of the corresponding classical system play an important role. Most physical systems are governed by nonlinear dynamics. Thereby the classical phase space (see the Poincaré surface of section to the right in the figure) exhibits both chaotic regions and regular islands. The centers of the islands (elliptic fix points) correspond to the stable periodic orbits (blue and red orbit in the left part of the figure; the black lines there are equipotential lines). The unstable periodic orbits (green orbit) correspond to hyperbolic fix points in the chaotic areas of the phase space.

The example chosen in the figure above is the famous Hénon-Heiles system. Its quantum level density exhibits characteristic shell structure that is successfully described in POT. For a recent publication, see:
M. Brack, P. Meier, and K. Tanaka: Uniform trace formulae for SU(2) and SO(3) symmetry breaking, J. Phys. A 32, 331 (1999).